High-precision spatiotemporal three-dimensional ultrashort pulse synchronization with optical Kerr effect
In studying the interaction of multiple ultrashort pulses with matter, such as plasma physics, inertial confinement fusion, and laboratory astrophysics, high requirements are put forward for spatiotemporal synchronization accuracy. However, these methods cannot simultaneously achieve high-precision, large-angle temporal synchronization and spatial overlap measurements of multiple short pulses.
Recently, a research team from Shanghai Institute of Optics and Fine Mechanics of the Chinese Academy of Sciences (CAS) experimentally demonstrated a method to achieve multiple ultrashort pulses temporal synchronization and spatial overlap measurements. The results were published in Optics Express.
In this work, the researchers proposed a method to achieve high-precision, three-dimensional (x, y, t) synchronization of ultrashort pulses at different angles by observing the transient phenomena of the optical Kerr effect. In the optical Kerr effect, the polarization state of the signal pulse changes only when it coincides with the pump pulse, at which point the signal pulse passes through the analyzer. The changes in the intensity and phase of the signal pulse is positively correlated with the degree of spatiotemporal coincidence. Since the phase of the transmitted wavefront of analyzer cannot be directly recorded by the detector, it needs to be reconstructed using a single-shot phase imaging algorithm. Coherent modulation imaging can achieve enhanced convergence performance due to the modulation effects of the encoding plate. The phase reconstruction algorithm utilizes the phase modulation information of the encoding plate and the diffraction pattern recorded by CCD as primary constraints. Through iterative calculations, the amplitude and phase information of the optical wavefront of the Kerr signal gradually approaching the true distribution can be obtained. Starting with an initial random guess, the complex amplitude distribution propagating to different planes can be calculated using the diffraction theory. The calculated values are replaced by the actual diffraction patterns recorded on the CCD. Subsequently, reverse propagation is performed with constraints given on the encoding plate, resulting in an updated wave function as the new guess. This process is iterated until the error condition is met, yielding the complex amplitude distribution of the Kerr signal, which reflects the temporal synchronization and spatial overlap between the pump and signal lights.
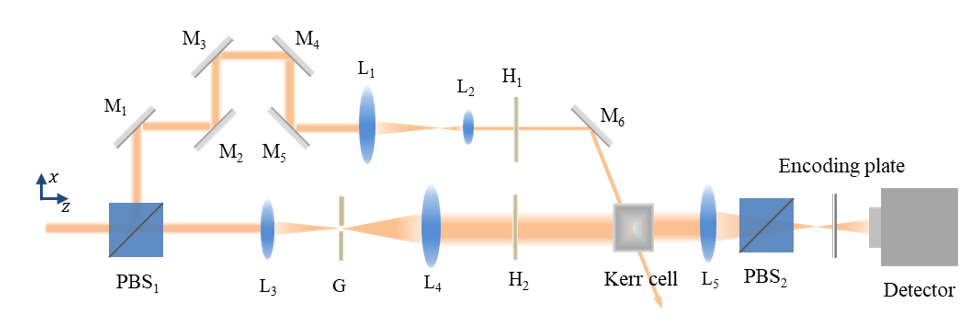
Fig. 1. Optical path diagram of ultrashort pulse spatiotemporal synchronization experiment.
In this study, 10-ps pulses were used in the experiments. By observing the intensity and phase distribution of the signal pulses, it is concluded that higher time synchronization accuracy can be obtained by observing the phase. Finally, the time synchronization accuracy between two pulses of less than 1 ps and spatial overlap accuracy of ±125 µm and ±3 µm in the x and y directions, respectively, were achieved. The spatial overlap accuracy depends on the step size precision of the translation stage used for synchronous adjustment and the CCD pixel size, respectively. The accuracy in the x direction can be improved by using a translation stage with a smaller step size. Moreover, the synchronization of two pulses at an angle of 90 ° was measured, further proving that the method can achieve the spatiotemporal synchronization of pulses with large angles. Therefore, this method has important application prospects in the study of multi-beam interactions with matter and other ultrafast physical phenomena. Furthermore, the effect of pump energy and signal pulse energy fluctuation was further analyzed. The results also showed that phase measurement is more stable than intensity measurement, which is conducive to the synchronous measurement of multi-beam pulses. This study provides a testing method for multi-channel laser spatiotemporal overlap measurements.
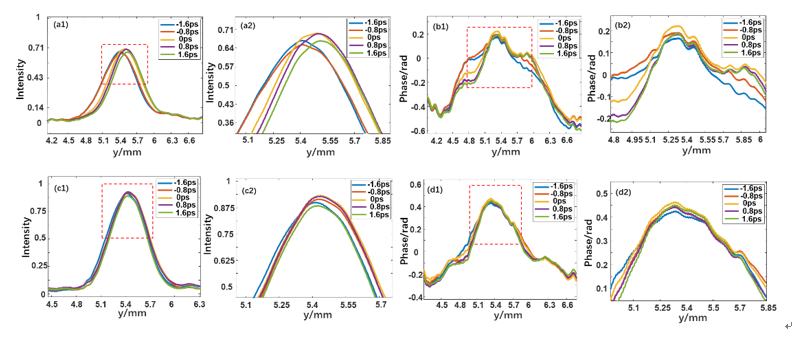
Fig. 2. (a1–a2) Spatial intensity and (b1–b2) phase change curves at different time delays and θ = 30°. (c1–c2) Spatial intensity and (d1–d2) phase change curves at different time delays and θ = 50°.
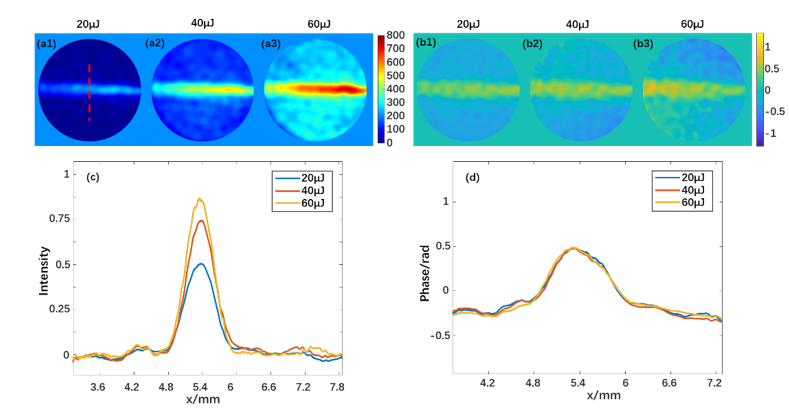
Fig. 3. (a1-a3) Intensity and (b1-b3) phase distributions of the transmission pulse at pump pulse energies of 0.1, 0.2 and 0.3 mJ. (c) Spatial intensity and (d) phase change curves at different pump pulse energies.
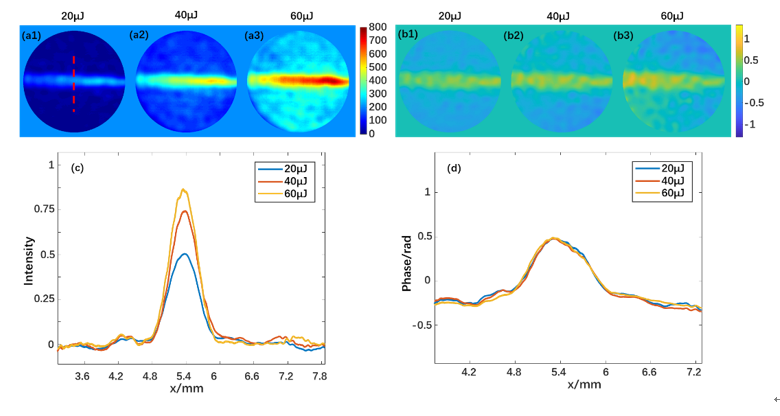
Fig. 4. (a1–a3) Intensity and (b1–b3) phase distributions of the transmission pulse under signal light energies of 20, 40, and 60 µJ. (c) Spatial intensity and (d) phase change curves corresponding to different signal light energies.